大気モデリング分野大気モデリング分野大気モデリング分野では、気候モデルに用いられる第２世代の大気大循環モデルを新しく開発することを中心に、数値実験を通して気候システムの秘密を解明するための研究を行っています。また同時に、ENSOに見られる気候システムの年々変動の予測・シミュレーションを行い得るような大気ー海洋結合モデルの開発も行っています。今後は、現在開発中の気候モデルを用いて、地球温暖化の評価を行います。
英語版へ
研究テーマ◆ 細かい格子の大気モデルの開発
◆ 積雲対流、地表近くの大気乱流など格子間隔以下の小規模現象の取り扱い
◆ ブロッキング現象など長続きする大気の特徴的な流れの形成機構
◆ 熱帯域の対流雲集団と大気の大規模な波動の相互作用
◆ 雲の形成過程や雲の放射特性の違いが大気の大循環に及ぼす影響
◆ 成層圏、中間圏の大気大循環が下層の大気に及ぼす影響
◆ エルニーニョ現象などの年々変動のメカニズム
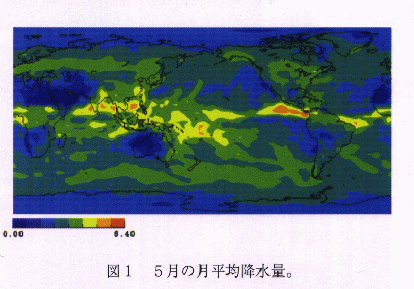
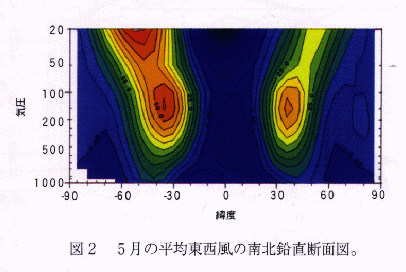
大気大循環モデルの現状現在の気候モデルは、雲・積雲対流の取り扱いと気候における海洋の役割を正しく表現する点で大きな困難をかかえています。両者とも、気候システム内部の水の循環に関連していることが興味深いところです。そこで、大気モデリング分野では、雲・積雲対流に見られる湿潤大気の振舞いを精度良く表現することを目指して第２世代の大気大循環モデルの開発を国立環境研究所（NIES）と共同で行っています。 その特徴は、 （1）気候モデルでは、放射過程の取り扱いが極めて重要であることから、放射過程にk-distribution 法に基づく新しいスキームを導入しました。このスキームは、長波と短波を統一的に扱っていることや、大気の吸収線のデータから精度を考えながらバンド数が選べることなど非常に汎用性の高いものとなっており、今後の温暖化問題等の研究に大いに役に立つと思われます。 （2）従来のモデルでは、放射における雲量と積雲対流過程で起きる凝結が統一的に扱われていない場合が多くありましたが、今回のモデルでは統一的に扱われています。そのために、新たに雲水量を予報変数として採用しました。 （3）水平・鉛直分解能もモデルの精度にとって非常に重要な要因です。当センターでは、出来る限り高分解能のモデルを走らせることを目指していますが、とりあえずは、T42（格子間隔250km程度）、鉛直は20層のモデルを基本として開発を進めています。 参考のために、我々のモデルの特徴を表1にまとめてあります。現在、最終的なパラメータの調整のために、様々な条件でモデルの性能を試験しているところです。図１はその一例ですが、静止状態の1月から積分を始めた時の5月の月平均降水量分布です。また、図２は東西平均した東西風の南北鉛直断面図です。南北両半球のジェットなどが良く表現されています。
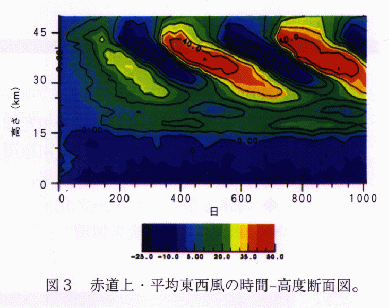
大気大循環モデルと数値実験数値モデルを用いた気候システムの力学の研究を平行して行っています。その一つは、今まで大気大循環モデルでは再現されなかったQBO（Quasi-Biannual Oscillation：準２年振動）を対象とした研究です。図３は高分解能のセクター・モデル（T106（格子間隔100km程度）45層）の結果ですが、QBOのように、東風・西風が順次下降して来ている様子が、３次元モデルで初めて再現されました。 もう一つの研究例は、気象庁数値予報課と協同して行っている、天気予報用の高分解能数値モデル（T213（格子間隔50km程度）30層）を用いた季節変化の研究です。この様な高分解能モデルの長時間積分は、世界で誰も行っていない研究であり、この研究によって気候システムの力学の秘密が明らかにできるものと思われます。
エルニーニョ現象の研究エルニーニョ現象などの年々変動を表現できる大気-海洋結合モデルは、大気大循環モデルの開発を踏まえて、平成６年度から本格的に開発に取り組む予定です。当面はENSOの予測と、海洋の４次元データ同化システムの手法の研究を考えています。 その他、TOGA-COAREのデータを用いた混合層の研究、対流のパラメタリゼーションの研究、semi- Lagrangian 法に関する研究などが行われています。
水平分解能 スペクトル法による三角形波数切断（T21 かT42）
鉛直分解能 20層
放射過程 DOM + k-distribution法
積雲対流 予測型のArakawa - Schubert
地表面過程 バケツモデル
地表のフラックス バルク公式による
境界層過程 Meller・Yamadaのレヴェル２のクロージャーモデル
重力波抵抗 McFarlane (1987)による
雲 雲水量を予報変数としている
時間積分 リープフロッグ方式及びセミインプリシット方式
CCSRホームページへ