複数の気候要素間のつながりを調べる上で, 線型の基礎解析である 回帰, 相関係数などは最も頻繁に使われる手法ですから, 早いうちに 覚えておくと便利です. ここでは例として2変数で説明しますが, 多変数でも基本は同じです.
回帰(一次単回帰)係数

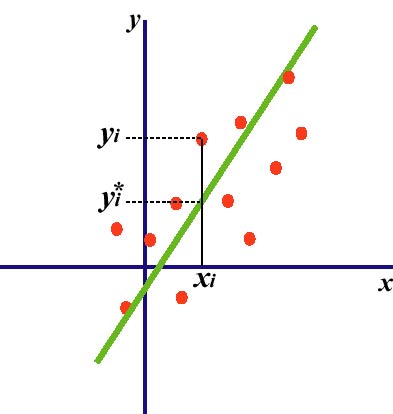
図1. 2変数間の線型モデル
従属変数yに対して引いた, 説明変数xによる一次曲線の傾きが回帰係数です. このとき, 直線のあてはめは任意に行うのではなく, yとy*(左図参照)の2乗和が最小になるように決めます(最小2乗法). 具体的には, 線型のモデル
を考え, 観測されたyとモデルのy*の差の2乗和S
のβに対する微分=0を満たすようにβ0, β1を決定します.
(4.1.17)から, 回帰係数はxとyの共分散をxの分散で割ったもの, となります. また, 我々が解析で扱うのは多くの場合偏差ですから, 切片β0はゼロとなり 意味をもちません.
トレンド
トレンドとは, 線型回帰においてx軸に時間をとった場合を特にそう呼びます. 例えば, 「ここ30年で全球気温に0.2°C/10年の正のトレンドがある」 といった具合に使われます.
ただし, 回帰, トレンドともにもとのx-y 関係が明らかに線型関係にない場合, 直線によるあてはめがそもそも 意味があるかどうかが疑問になってきます. ですから, x-yの散布状態を 見ずに, やみくもに回帰係数だけを計算して議論を進めるのはよいやり方ではない. このとき, 得られた回帰係数の「統計的」意味付けの指標になるものの一つが 相関係数です.
相関係数
相関係数はその名の通り, 変数間の関連の強さを表す統計量で, xとyの共分散をx, yそれぞれの標準偏差で割ったものと定義されます.
回帰係数と違って無次元量で, -1から+1までの値をとり(証明は統計のテキストを参照), 線型モデルに対するデータのばらつきを意味します. 例えば, 下の左図のように 同じ回帰係数であっても, ばらつきが大きくほぼ円形にサンプルが分布していれば(r〜0), 得られた回帰係数は信頼できないと言えます(サンプルが一つ増えただけで回帰直線 の引かれ方が大きく変わる可能性が高い).
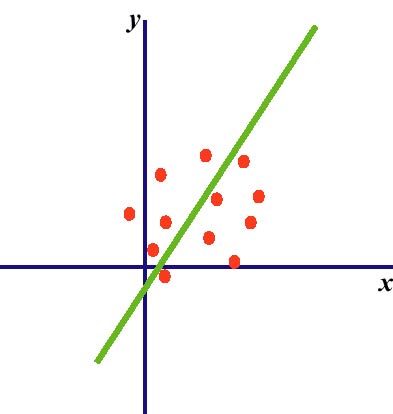
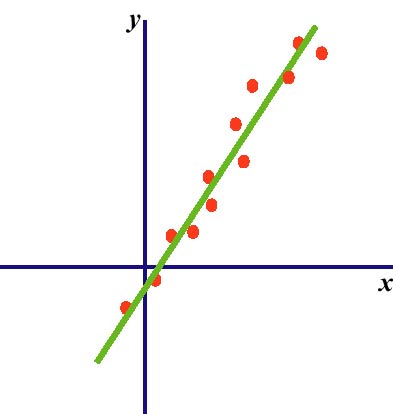
図2. 2変数間の線型モデル(左:2変数はほぼ無相関, 右:高い正の相関)
相関係数の式(4.1.8)は, xとyをベクトルとみなしたときの内積に等しい. すなわち, 図3のように変数ベクトルx, yのなす角をθとすると r=cosθである. 従って, r=1はx,yが同じ向きである場合に, r=0は直交している 場合に相当する.
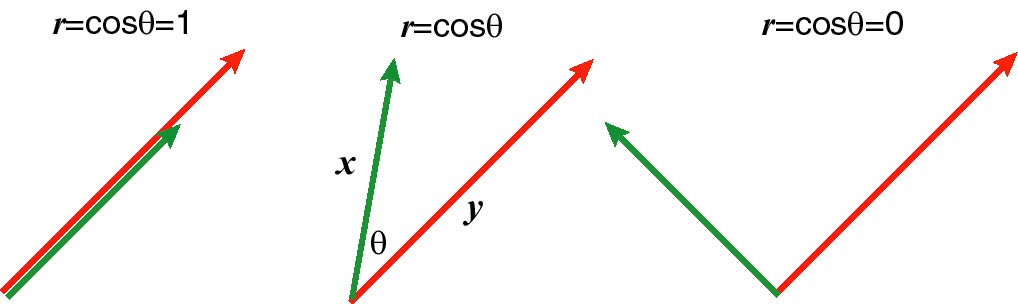
図3. 位相空間での相関係数
気候とその変動現象に相関・回帰解析を適用するときに, 注意しなければいけないことが いくつかあるが, ここではそのうちの2つを挙げるにとどめる.
気候システムは多変数からなる系である. 従って, そのうちのある2変数間が 高い相関を示すからといって, ただちに因果関係には結び付かないかも しれない. 例えばエルニーニョが日本とアメリカの気温に影響している とすると, 日本とアメリカの気温には正相関が予想されるが, この場合 そこに因果関係はなく, 両者ともにエルニーニョの従属変数である.
ある2変数間に相関がないからといって, ただちにその変数同士は 関連がないと決められないかもしれない. というのは, (4.1.8)は 変数間の時間的ずれ(ラグ)を考慮していないからである. 例えば sinθとcosθは相関0であるが, cosθをπ/2時間方向にずらしてやれば 相関は1である. 気候においては, 波による伝播, 移流, サブシステム間の 応答時間の違い, などがラグを生じることが多いので注意すべきである.
 必要ならばサンプルプログラムopcor.fとMakefileをコピー
して使ってもOK. 計算結果のデータをGrADSで見るための.ctlファイルはここ.
必要ならばサンプルプログラムopcor.fとMakefileをコピー
して使ってもOK. 計算結果のデータをGrADSで見るための.ctlファイルはここ.
で表されるモデルをn次のマルコフ過程, あるいは自己回帰過程(AutoRegresssive process, AR(n))と呼ぶ. εはホワイトノイズである. 特に, AR(1)
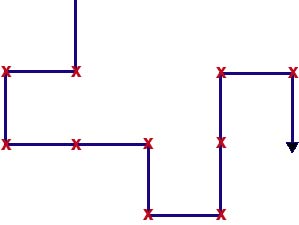
図4. 2次元の酔歩の例
でa1=1のときを酔歩(ランダムウォーク)と言う. これは, 図4のように2次元で
表現した(4.3.2)の軌跡があたかも酔っ払いの千鳥足そっくりだからである.
(4.3.2)は, 物理的には
(但しw(t)はホワイトノイズ, λ>0) というランダム強制のもとでの減衰方程式 (stochastically-forced decay equation)を有限差分化した形
と同じである. (4.3.3)は単純化した気候(あるいはそのサブシステム)のモデルと してしばしば使われる. w(t)は日々の天気に相当するような時間 スケールの短い気象現象を表現し, λは対象(例えば海洋の温度変動)の時間スケール ("メモリ"), といった具合である.
[作業2] 平均0, 分散1であるようなεの時系列(N=500)が~hiro/public/data/にあります.
[/home/maro/data/%] cp ~hiro/public/data/random500.grd . [/home/maro/data/%] cp ~hiro/public/data/random500.ctl .
と自分のディレクトリにデータと.ctlファイルをコピーした後, この時系列
を用いて, 任意のa1 (a1>1ではどうなるかな?)に対するAR(1)時系列を
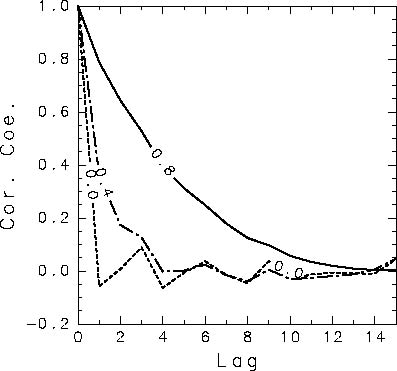
書いてみましょう. また, その自己相関関数のグラフを書いてください
(こういうグラフには電脳が向いていますから, DCLで描きましょう).
関数を描くサンプルプログラムは
ここにもあります. 結果は例えばこんなグラフになります(a1=0.0,0.4,0.8
の各々についてプロット). a1とλの関係が分かりますか?
今, wはホワイトノイズであるからFw^2はωによらない. 従ってスペクトルの
形はλだけに依存する. ω>>λの高周波領域ではスペクトルはωの-2乗に比例
するような傾きをもつが, ω>>λの低周波領域ではPはほぼ定数となる.
これが赤色ノイズのスペクトルで, (4.3.3)の減衰項は従って白色ノイズを
赤色ノイズに変換するフィルターの役割を果たすことが分かる. パワースペクトル
については4.5を待て.
(4.3.3)をフーリエ展開し, 2乗してパワースペクトルP(ω)を求めると,
t検定
相関係数をrとしたとき, 以下のように定義される統計量tは自由度νのt分布に従う.
ただしν=N-2. (4.4.1)から,
となるので, 有意水準αを満足する相関係数は
となる. 検定の手順は以下の通り.
互いに独立でない要素x=(x1,x2,...xN)からなる集団のサンプル数を, Nのかわりに effective sample size, Neで定義する. NeはT0をcharacteristic time scaleとして
ただし
ここでr(τ)はラグτの自己相関関数.
[作業3] 4.2で描いた一点相関のt検定をしてみましょう. 結果は, 4.2の例のように相関図に 重ねて描きます. ただし, 自由度と(4.4.1)のtを入力して相関係数の有意水準を出力に返す function, t-test.f が使えます.
ランダムな要素の強い気象・海洋データでは, ちょうど[作業2]で作ったAR(1)の時系列
のように一見しただけではそこに何らかの周期性が含まれているかが分かりません.
そこで, データの時間変動特性を知るためにパワースペクトルを計算して
図示することがあります. 以下に述べるように, パワースペクトルは
4.1の相関係数と独立なものではなく, 4.3で使った自己相関関数によって
互いに結びつけられています.
フーリエスペクトル
簡便のために, x(t)を連続な無限関数とする. 任意のxに対して, 次のような フーリエ変換, フーリエ逆変換によって周波数ωの関数であるフーリエ係数 C(ω)が関係づけられる(関数が不連続, 有限の場合, (4.5.1)(4.5.2)は Gibbs現象にため可逆過程とはならない).
C(ω)は周波数ωの波の振幅を表す. そのエネルギー, すなわち2乗した もの
をパワースペクトル密度(power spectrum density)と呼び, P(ω)などと 書く.
パワースペクトル密度は, 次のように自己相関を用いても定義できる. 自己相関関数ρ(τ)をまずこう書く.
(4.5.4)に(4.5.1)を代入し, (4.5.2)の共役を用いると, ρとPの関係式
(Wiener-Khintchine公式)が得られる.
すなわち, 自己相関関数はパワースペクトルのフーリエ変換である. 従って, ρが分かっていればフーリエスペクトルが描けるし, 逆もまたしかりである.
FFT
実際の有限データのフーリエ変換は, (4.5.2)の離散形で求められる. このとき, Nをデータの長さとすると計算量は約N*Nである(n番目の 周波数成分を計算するのに, N回の計算が必要). これは, Nが大きいときには 非常に時間がかかる. (4.5.5)を用いて自己相関関数からスペクトルを 求めるやり方をBlackman-Turkey法というが, その場合でも計算量は N*N/2程度かかる(aliasingを避けるため, Blackman-Turkeyではナイキスト周波数1/2Δtまでしか 計算しない). そこで, 現在では 高速フーリエ変換(Fast Fourier Transform, FFT)と呼ばれるアルゴリズム が主流になっている(最大エントロピー法というのもありますが, ここでは 触れません). FFTに要する計算時間はほぼNlogNで, 例えば N=10^6だとすると通常のフーリエ変換で2週間かかる計算がFFTでは30秒 で終ってしまう!
FFTの原理は, Nに2のベキ乗を選んだ場合にはフーリエ変換の係数行列に i, 1, -i, -1が交互に現れるので行列を分解できるという ものである(詳しくは「スペクトル解析」朝倉書店などを参照). 有限の時系列xを用いたパワースペクトル計算の 具体的な手順は,
となる.
実際にスペクトル解析を行う際の注意点. FFT 適用前にトレンドを除去すること, 特定周期のスペクトルが 卓越し過ぎるときには事前にその成分を除いておくこと(プレホワイトニング). プレホワイトニングは目的によっては 必ずしもやらなくてもよい.
[作業4] 4.3で作ったAR(1)のパワースペクトルを 計算して, DCLで描いてみましょう. また, (4.3.2)にcos(2πkt/N)のような周期的強制を加えて, スペクトルを計算してみましょう. 加えた周期に対応するωでパワーが増大していれば OKです. FFTにはDCLのMATH2ライブラリにある サブルーチンRFFTFを使います. 用法は
REAL X( N ) REAL WSAVE( 2*N+15 ) .... CALL RFFTI( N, WSAVE ) !! 初期化 CALL RFFTF( N, X, WSAVE ) !! FFT (Xは入力/出力配列)配列Xは入力時は時系列ですが, 出力時にはフーリエ係数が格納されており, 並びは
X=(A0, A1, B1, A2, B2, ..... AN/2) :Nが偶数時 X=(A0, A1, B1, A2, B2, ..... AN/2, BN/2) :Nが奇数時です. パワースペクトルは例えばこのような図になります(左:DCL版, 右:GrADS版). 実際に研究に用いるスペクトル解析では, さらに各種の平滑化処理を行うことも多い.
パワースペクトルの有意水準