海洋大循環モデル開発

海洋の大規模な循環を扱うための数値モデルを海洋大循環モデルと呼びます。その概念的なことについては「海洋循環のモデリング研究」に述べてあります。ここでは、我々の開発している COCO という名称の海洋大循環モデルを例にとりつつ、より具体的な開発の実態について述べます。

海洋大循環モデルの開発は

• モデルの枠組み
• 数値計算アルゴリズム
• パラメタリゼーション

の開発に大きく分けられます。海洋大循環モデル開発は世界中の諸機関で日進月歩で行われており、常に最先端のモデリング研究を続けていくためには、少なくともそうした世界的な動向に遅れをとらぬようにモデルを維持する必要があります。COCO の開発は、大気海洋研究所（旧気候システム研究センター）海洋グループと海洋研究開発機構先端的海洋モデリング研究チームのメンバーをはじめとした多くの手によって、絶え間なく続けられてきています。

海洋大循環モデルに必要とされる開発要素は実に多岐にわたるものなので、そのすべてを個人あるいは単一機関で一から行うのは不可能です。実際の海洋大循環モデル開発の現場では、他の研究者が提案したものや他分野で用いられている手法の導入が主たるものとなりますが、それぞれのモデルにはそれぞれの特性があるので、既存のものを導入するだけでも決して簡単なことではありません。

モデルの枠組みの開発

海洋大循環モデルが基礎としている方程式系は、回転球面上の流体力学の運動方程式、熱力学の方程式（熱力学第一法則と状態方程式）、および溶存物質の輸送方程式です。このうち運動方程式には、表現する現象の規模に関する考慮に基づいて、計算効率を良くするためのいくつかの近似が施されています。モデルの枠組みとは、どのような近似を採用するのか、方程式系をどのような座標系のもとで定式化するのか、そして境界の扱いをどのようにするのかという、 解くべき方程式系の決定と境界条件の与え方に関する部分です。また、それらの方程式系を計算機上で解く場合には離散化を行う必要がありますが、その方法として何を用いるのかについてもモデルの枠組みにあたる部分です。

例えば、水平座標系の選択を例にとってみます。地球上の水平座標を表現するのに最も一般的で簡単な座標系は経度と緯度による球面座標系です。球面座標系で定式化された方程式系を差分法を用いて離散化する場合には、通常、地球上を経度線・緯度線で格子に区切り、その格子点上の値を計算機を用いて計算することになります。しかし、地球儀などを見てわかる通り、北極点付近と南極点付近で経度線が集中し、そこでの格子幅は低緯度に比べて非常に小さくなります。理由は省きますが、これは数値計算上の困難をもたらします。南極点は幸いにも南極大陸上に存在するために気にする必要がないのですが、北極点は北極海の真ん中にあり、これをこのままにして数値計算を遂行することは実質的に不可能です。

海洋大循環モデル開発の歴史は1960年代にまで遡ることができますが、当初から1990年代半ばにいたるまで、世界中で開発されて使われていた海洋大循環モデルのほぼすべては水平座標として球面座標系を採用していました。そうしたモデルでは、北極海をつぶしてしまって全く表現しない、北極点の周りに人為的に陸を置くなどの方法が初期はよく採られていました。しかし、海洋大循環や気候における北極海の重要性に鑑みて、北極海をモデルで正しく表現することに対する要請は大きなものです。

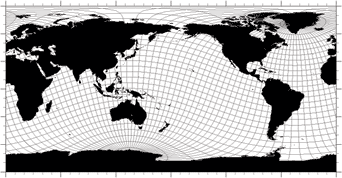
このため、球面座標系を回転させて座標線が集中する特異点を陸上に移動させるという方法が採られることがあります。回転させた座標系の座標値は地理的な経度・緯度ではなく なるわけですが、球面座標系上で定式化されているということに変わりはないので、方程式系の変更が一切必要でないというのがこの方法の利点です。一方、この方法では、ふたつの特異点を同時に陸上に持ってくる方法に制約があります。というのも、一方の特異点は必ず他方の特異点から最も遠い位置にあるので、一方の特異点の置き場所を決めるともう一方の特異点の置き場所も自動的に決まり、その両方が陸上にくるようにするやり方には限りがあるからです。図1は球面 座標系の回転によって、北極の特異点をグリーンランド上に移動させた場合の座標線の例です。この例ではもう一方の特異点も南極大陸上に存在し、海洋上には特異点が存在しないような座標系が実現できています。

図1: 球面座標系の回転の例。

最近の海洋大循環モデルの多くは、水平座標系として一般曲線直交座標系を採用しています。球面座標系は球面上の曲線直交座標系のひとつで、その中でも最も自然で簡単なものです。一般曲線直交座標系で方程式系を定式化し、具体的に用いる座標系を構築するためには、テンソル解析や複素解析の知識を応用します。球面上を単一の座標系で表現する場合、座標線の集中する特異点が必ず存在します。したがって、どのような座標系を使おうとも特異点を陸上に置くという措置が必要になるわけですが、一般の曲線直交座標系を用いれば、 すべての特異点をそれぞれ任意に選んだ陸上に置くことが可能です。一般に特異点の近くは解像度が高く表現されることになるので、比較的高い解像度で表現したい海域の近くの陸上に特異点を置くという選択を行うことができます。図2は北米大陸上とユーラシア大陸上に特異点を置いた曲線直交座標系の座標線の例で す。この例では北極海が比較的高解像度で表現されます。直交座標系という制約があるため、座標系を好き勝手に設定できるというわけではありませんが、球面座標系の回転に比べればできることは飛躍的に多くなります。直交座標系という制約を外せばより自由な座標系の設定が可能になるわけですが、その一方で方程式系の表現が格段に複雑になってしまいます。

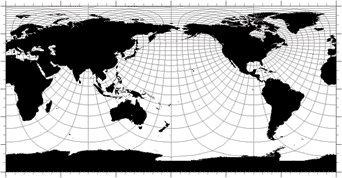
図2: 一般曲線直交座標系の例。

水平座標系に関することは、海洋大循環モデルの枠組み開発に関するほんの一例にすぎません。この他にも、鉛直座標系、離散化手法（有限要素法など）、海岸線や海底地形の表現方法などの様々な面について、物理的要請や数値計算技法の進展に応じた開発が世界中で進められています。

数値計算アルゴリズムの開発

海洋大循環モデルの基礎方程式系は時間と空間に関する偏微分方程式系で表されます。数値計算のためにはその方程式系を離散化する必要がありますが、離散解法には様々な種類の誤差がつきまといます。解像度を高めれば誤差を減らすことができますが、同じ解像度でも用いる数値計算アルゴリズムによって誤差は変わります。一般に誤差の少ない数値計算アルゴリズムほど計算負荷が高いものなので、闇雲に高性能なアルゴリズムを使うことはできず、対象とする現象や用いる解像度に応じて適切な数値計算アルゴリズムを選択することが必要になります。

図3は水温や塩分の移流（流れによる輸送）に関する数値計算アルゴリズムとして精度などが異なる3種類のものを用い、解像度などその他の条件は同じにして行った海洋大循環モデリングの結果です。移流を数値計算で正しく解くためには、精度以外にも非分散性（移流の過程で振動を生じないこと）や形状保存性（移流の過程で形が崩れないこと）などが重要となります。この例の右の結果に見られるように、単に精度が高いだけで妥当な結果が保証されるわけではありません。

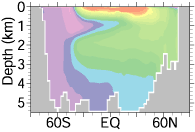
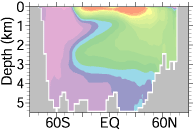
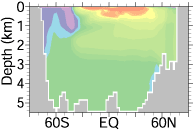
図3: 異なる移流アルゴリズムを用いて行った海洋大循環モデリングにおける大西洋東西平均塩分。赤に近いほど高塩分、紫に近いほど低塩分。左は精度が高く分散性の低いアルゴリズム、中央は精度が低く分散性のないアルゴリズム、右は精度が高く分散性の高いアルゴリズムによる結果。水深 1 km 付近に見られる低塩分水の貫入が、左の結果で最も現実に近く、中央の結果では深くぼやけた構造に、右の結果では表現されていない。Hasumi and Suginohara (1999) の結果より。

先ほど解像度が高まれば数値計算に伴う誤差は小さくなると述べましたが、その意味には注意が必要です。全く同じ現象を表現している限りにおいては、解像度が高いほど数値計算に伴う誤差が小さくなるのは真実です。しかし、海洋には様々な空間スケールを持った現象が存在し、解像度を高めていくと、それまでは表現できなかった小さな空間スケールの現象を表現できるようになります。例えば、海洋には中規模渦と呼ばれる水平数十 km スケールの渦がいたるところに存在 しますが、海洋大循環モデルの水平解像度が 100 km 程度より低い場合（全球海洋のモデリングではその程度の解像度は今でも一般的です）には、これらの中規模渦を表現することができません。中規模渦に伴う流速はより大規模な空間スケールの流れと比べて大きなものです。移流に伴う誤差は一般的に流速とともに大きくなります。したがって、解像度が高まって新たに中規模渦が表現できるようになると、強い流れを表現するようになるため、それに伴う数値誤差を抑えるためには却って高い精度の数値計算アルゴリズムを用いる必要すら生じます。そうしなければせっかく高解像度にした利点がなくなってしまい得るのです。現在の海洋大循環モデリングは、世界的にどんどん高解像度の方向に向かっていますが、それに伴って数値計算アルゴリズムに対する配慮の重要性もますます高まっています。

パラメタリゼーションの開発

先ほども述べたように、海洋には様々な空間スケールを持った現象が存在し、そして数メートルという空間スケールを持つ現象でも全球規模の海洋の状態と無縁ではありません。先ほどの中規模渦を例にとって考えると、中規模渦は形成されてから減衰していく過程において水平方向に熱や溶存物質を輸送する働きを持っています。この中規模渦に伴う輸送は、海洋の大規模な構造を決める上でも欠かせない役割を果たしています。海洋大循環モデルにおいてこれらの中規模渦が表現されないということは、それに伴う輸送が表現されないということで、現実的な海洋シミュレーションを行うことができないことにつながります。

中規模渦を表現するような解像度は、現在の計算機事情で不可能ではありませんが、全海洋を扱うような場合には決して容易ではありません。また、たとえ中規模渦を解像しても、それよりもさらに小さな表現されない現象がまだまだ存在します。海洋に存在する全ての現象を表現することはまず不可能で、実際のモデリングにおいては必ずなんらかの表現されない現象が残ります。したがって、それら表現されない現象がより大きな空間スケールの流れや構造に対して及ぼす影響を採り入れる必要があります。その表現には理論的あるいは経験的に得られるいくつかのパラメータが用られ、そのような手法はパラメタリゼーション（パラメータ化）と呼ばれます。

ここでは COCO に組み込まれている海底境界層パラメタリゼーションを例に取り、より具体的な適用例を紹介します。ここでも解説しているように、全球海洋の深層を占める深層水は空間的に非常に限られた領域で形成されていますが、それらの領域のほとんどは大陸棚上や縁辺海にあり、形成された深層水が外洋に流れ出る過程では大陸斜面上を下ったり海底山脈を越えたりします。こうした斜面を下る流れは、ただ単に重い（密度が高い）水が重力の作用で下に落ちるというものではありません。地球の回転の効果は斜面を下る流れを抑え、流れが斜面の同じ深さに沿うような水平的なものにする働きを持つからです。それにも関わらず現実には斜面上を高密度水が下っているのですが、そこでは斜面上に存在する高密度水とその上の低密度水の境界で生じる渦運動生成がとても大切な役割を果たしています。この渦運動をモデルで表現するためには、中規模渦を表現する以上の水平解像度が必要とされます。また、鉛直座標系として深さを用いている海洋大循環モデル（既存のものの大部分はそうです）では斜面が階段状に表現されることになり、斜面に沿って生じる現象を表現するのに困難があります。これを表現するためのものが海底境界層パラメタリゼーションです。

水平解像度1度の海洋大循環モデルにおいて、海底境界層パラメタリゼーションを適用するかどうかでグリーンランド海で形成された深層水の北大西洋への流れ出しがどのように違うのかを示したのが図4です。ここで用いた海底境界層パラメタリゼーションでは、海底直上の格子が海底境界層を表現しているとみなし、 水平方向に隣り合う格子の海底境界層はその深さが大きく離れていても直接水を交換するようにして、斜面に沿う流れを表現しています。また、渦の働きの結果として流れの方向がどのように影響を受けるのかをひとつのパラメータで表現しており、そのパラメータの値は高解像度で行われた斜面降下流を陽に表現できるモデルの結果に合うように決められています。こうした深層水流出は全球規模の深層循環にとって重要なもので、そのモデルにおける表現のためには、海底境界層パラメタリゼーションはなくてはならないものです。

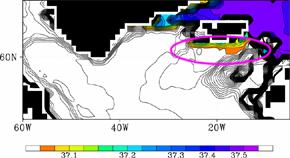
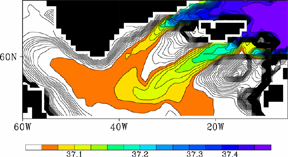
図4: グリーンランド海で形成された深層水の北大西洋への流れ出し。左は海底境界層パラメタリゼーションを適用しなかった場合、右は適用した場合。色は海底直上 の海水密度で、寒色ほど高密度。海底境界層パラメタリゼーションを適用しないと、高密度水の流れ出しが表現できない。Nakano ahd Suginohara (2002) の結果より。

必要なパラメタリゼーションとしては、この他に、海面混合層、中規模渦、鉛直対流、内部 潮汐など、様々なものがあります。これらのうち多くのものには既存のパラメタリゼーションが存在し、ある程度の成功がおさめられていますが、それでも解決 すべき課題はいまだに多く存在し、さらなる開発が世界中で続けられています。

ひとつ上に戻る